Abstract
Regressor-based modeling of nonlinear systems yields a parameterized equation describing the dynamic of the system. The existing robust control approaches mostly account only for uncertainties present in the parameter vector, while the unmodeled dynamics and perturbations in the regressor matrix could significantly deteriorate the controller's performance. In this article, we propose a novel robust control approach with safety considerations that also accounts for uncertainties in the regressor matrix and the parameter vector. Herein, we design a control law comprised of several signals that ensure uniform ultimate boundedness of the known dynamics via Control Lyapunov Functions, forward invariancy of a desired safe set via Control Barrier Functions, and a switching law that cancels out the effects of uncertainties in the system's model. Stability and safety analysis are validated with a numerical simulation, showcasing the implementation and versatility of the proposed control design. The framework's robustness is also challenged in a Monte Carlo run, and the algorithm shows robustness to random perturbations in the modeling uncertainties.
The Challenge: Models Are Never Perfect
Controllers rely on mathematical models to predict how a system will behave. A common modeling technique separates a system's dynamics into a known structure, called a regressor matrix, and a set of unknown physical properties, like mass or friction, called a parameter vector. The problem is that most "robust" controllers only account for uncertainty in the parameters, assuming the model's structure is perfectly accurate.
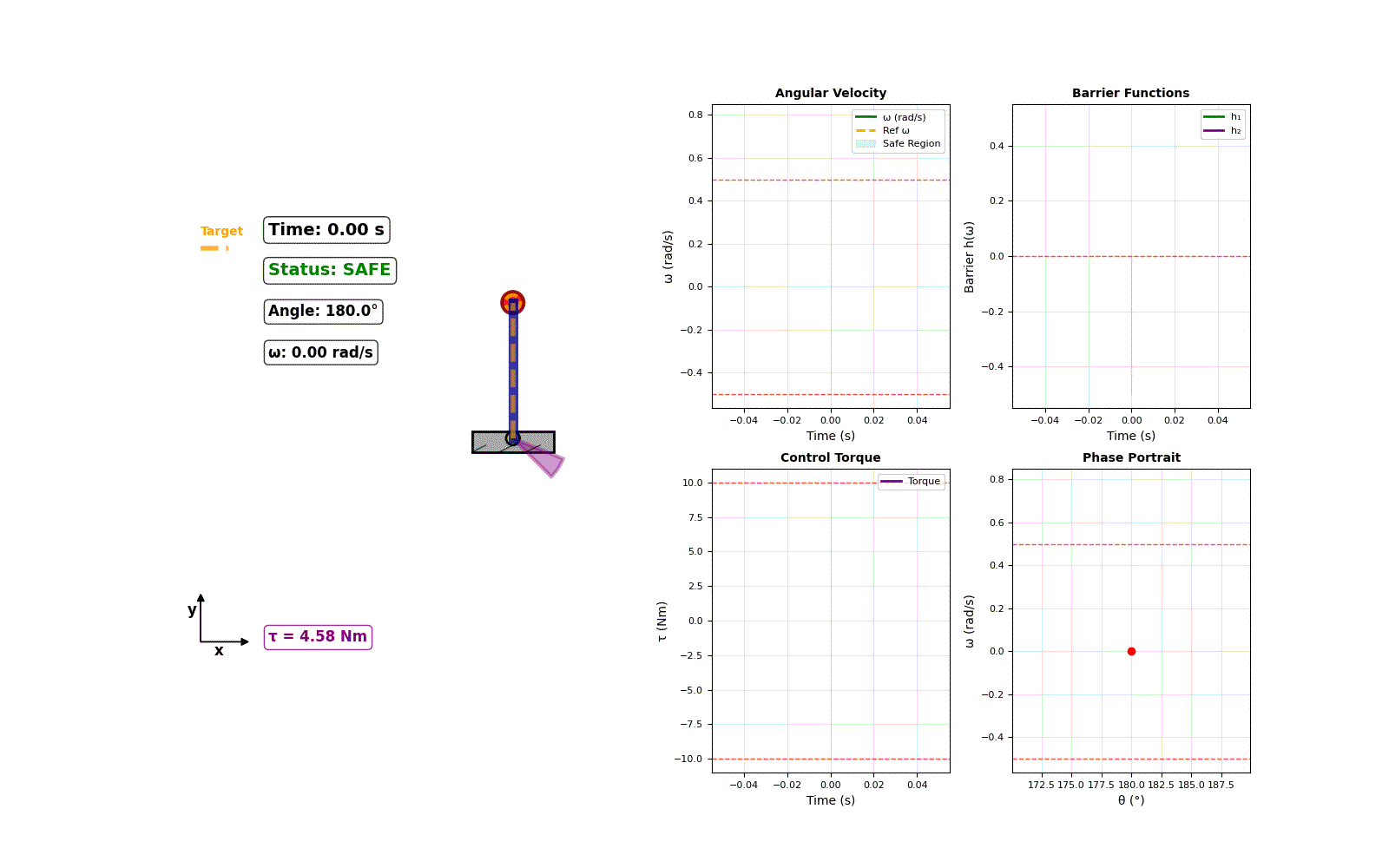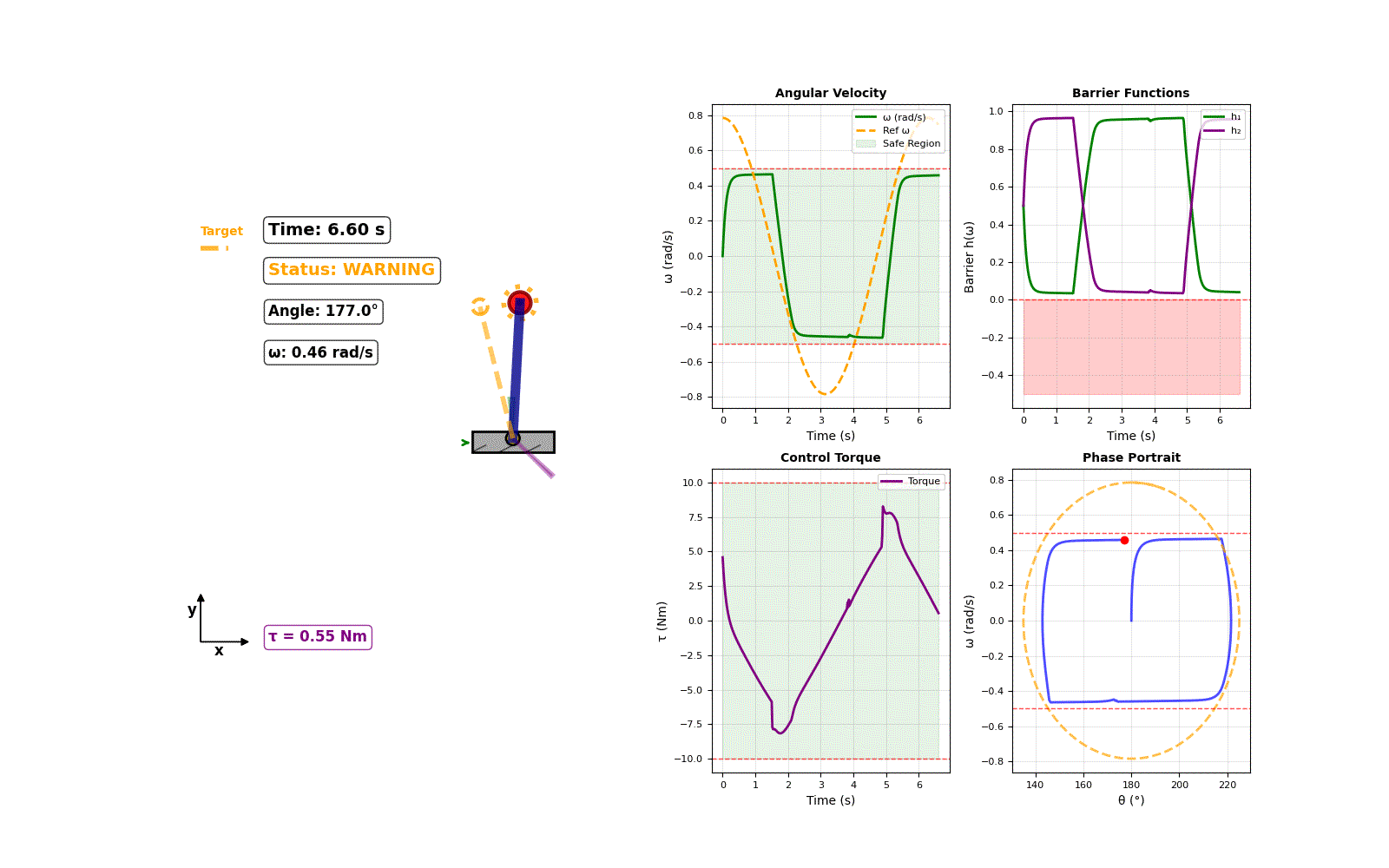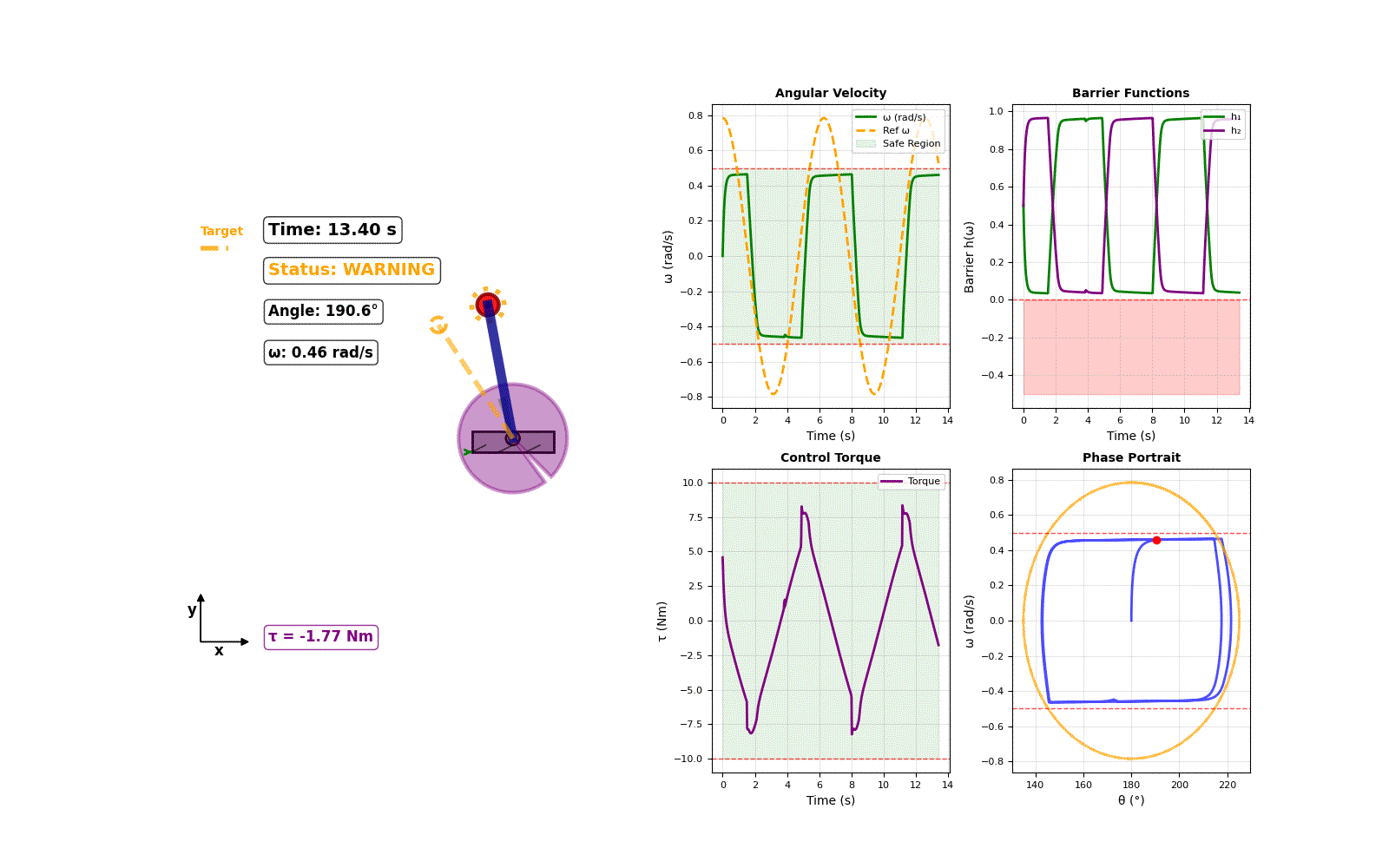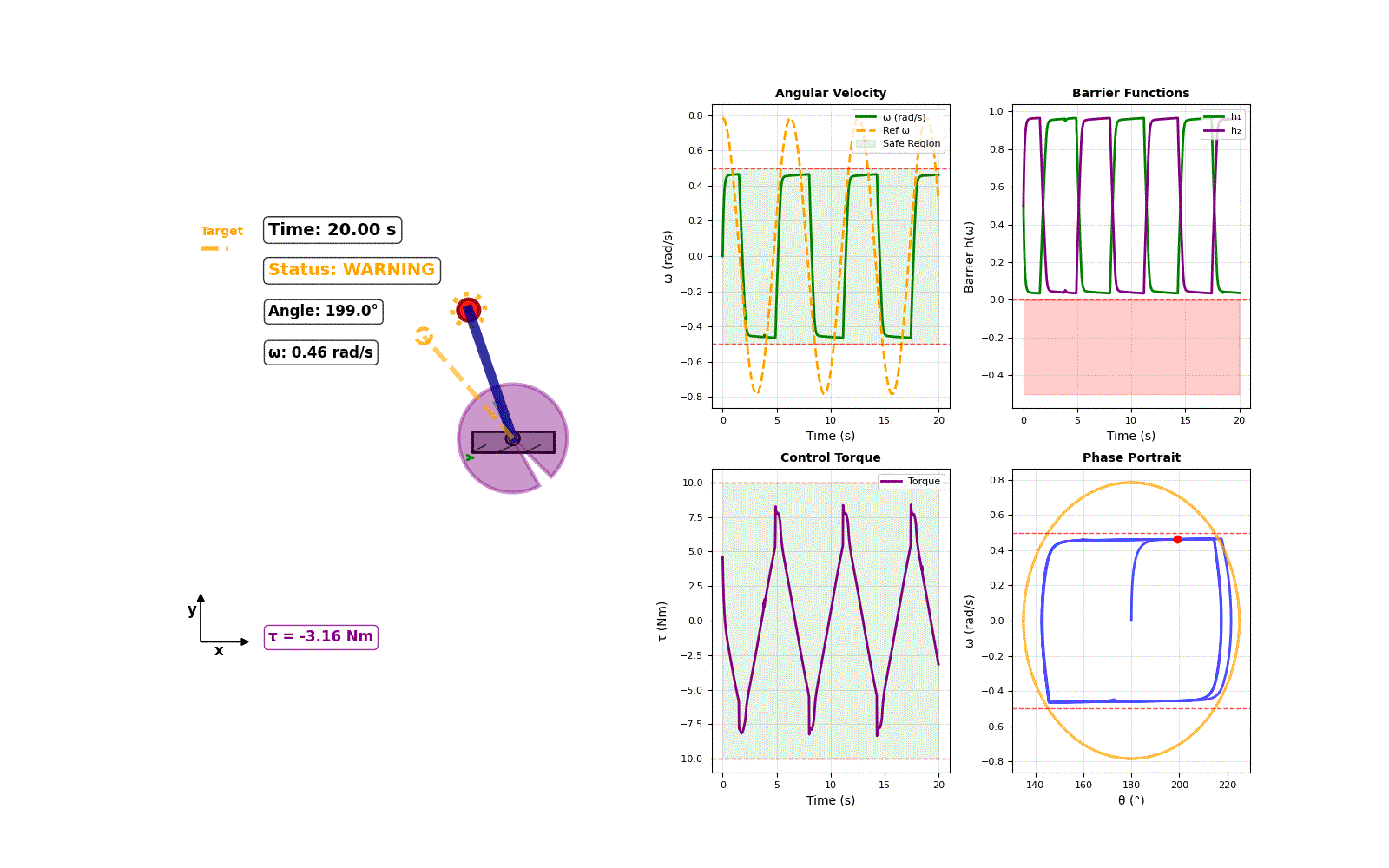
In reality, this assumption is often false. Unmodeled effects and sensor noise can introduce errors into the regressor matrix itself, which can severely degrade a controller's performance or even cause it to fail. Our work addresses this critical, often-overlooked source of uncertainty.
Our Solution: Handling Deeper Uncertainty
We designed a novel control law that explicitly accounts for uncertainty in both the regressor matrix and the parameter vector. Our controller intelligently combines three key components into a single real-time optimization problem (a Quadratic Program):
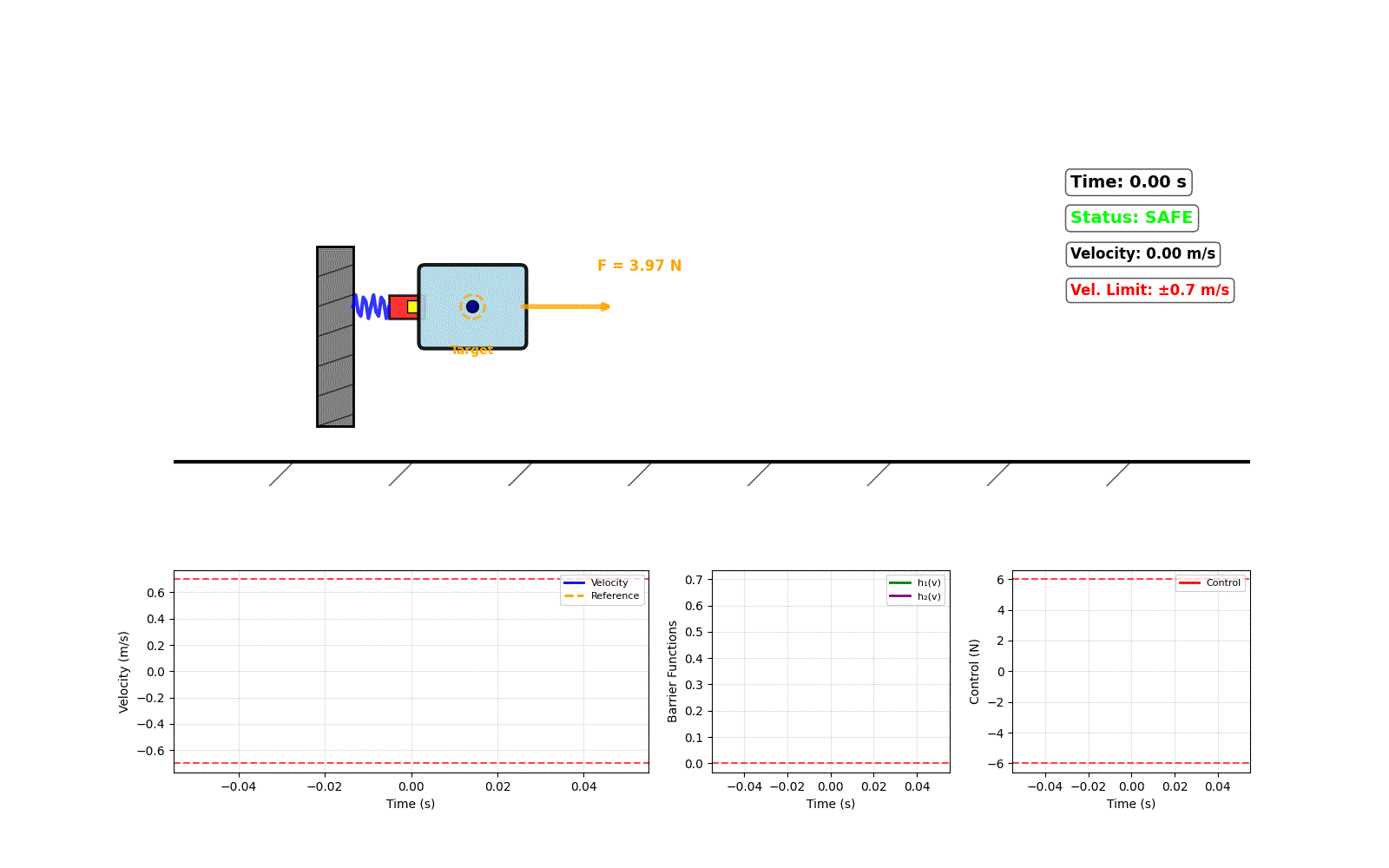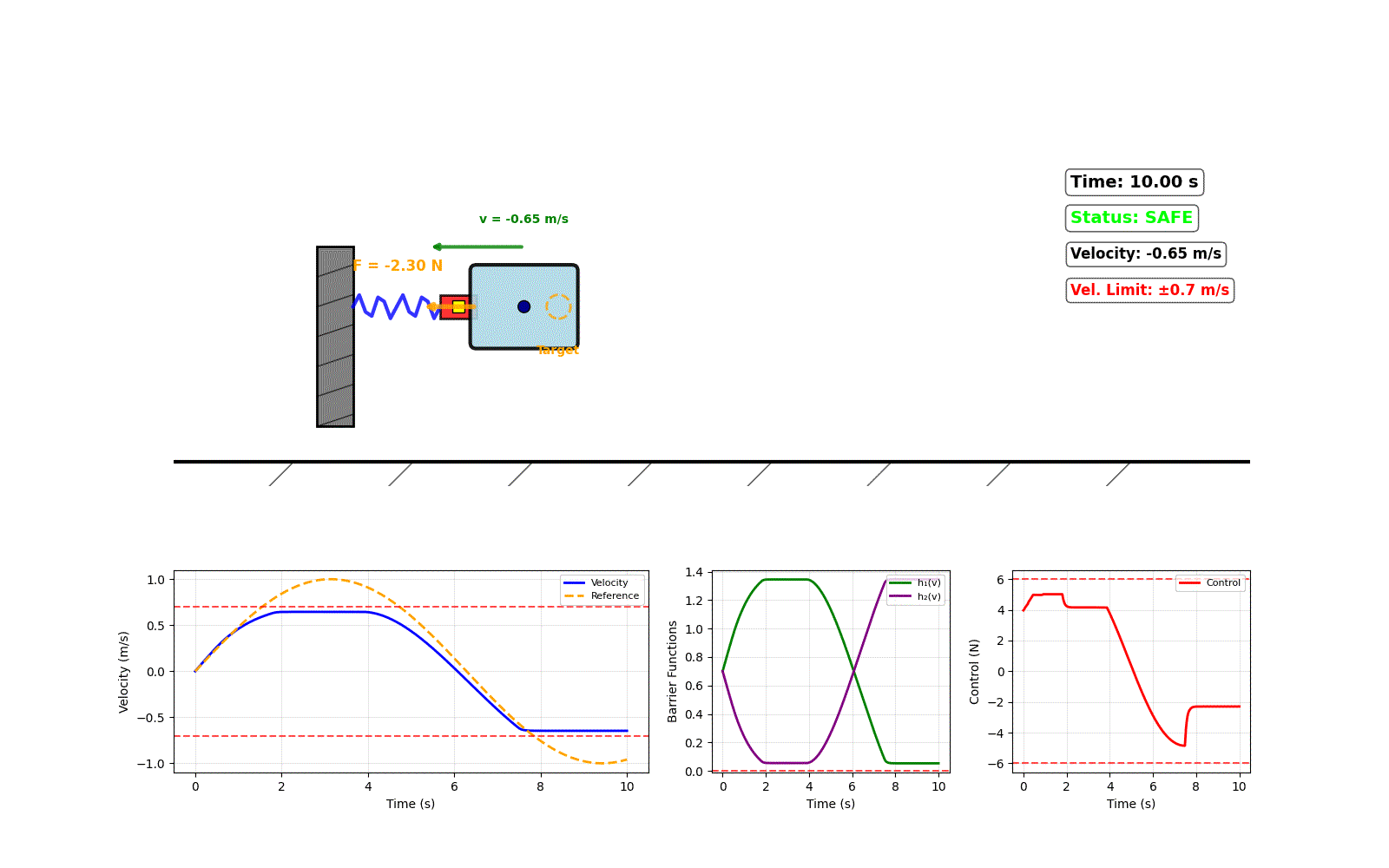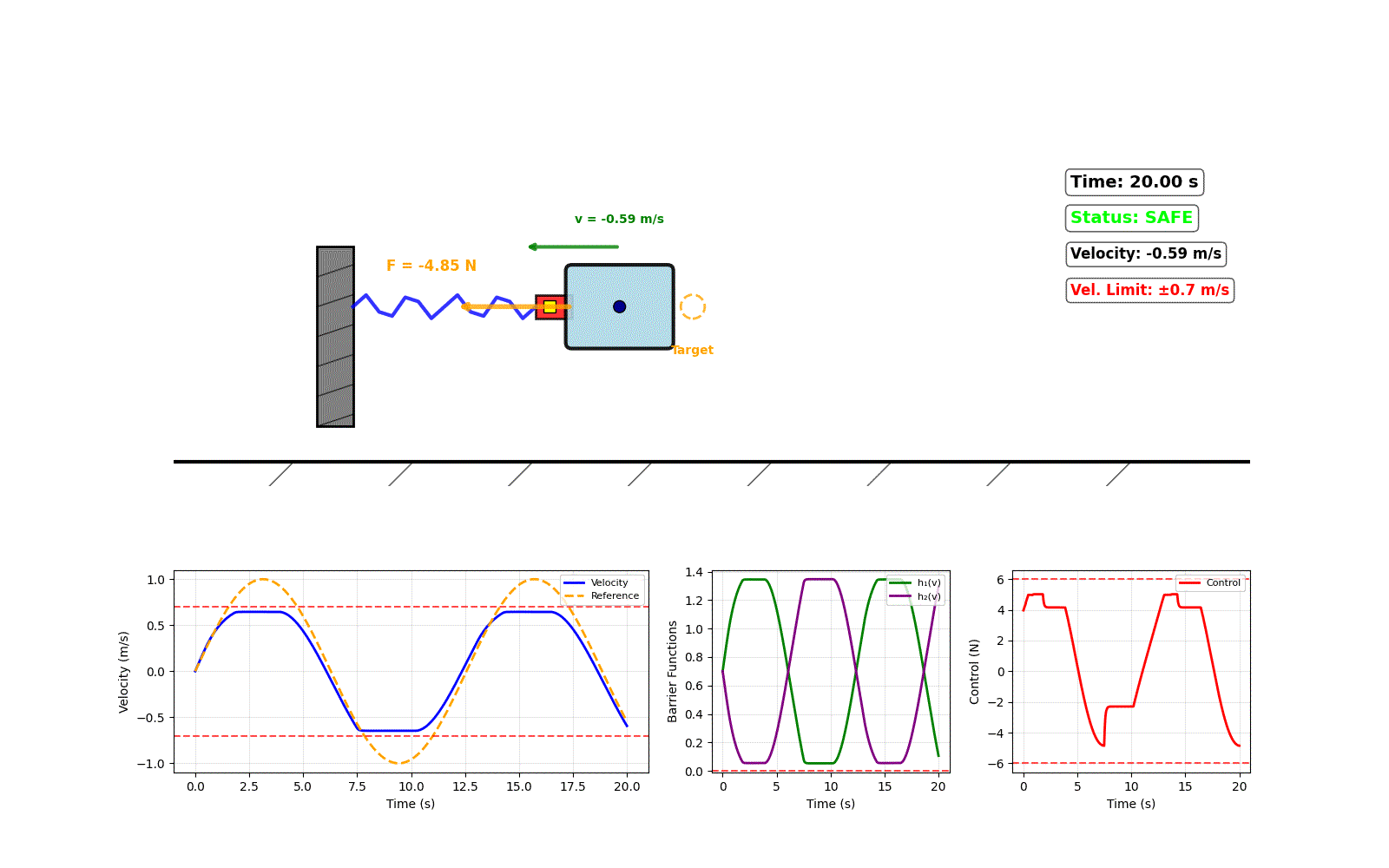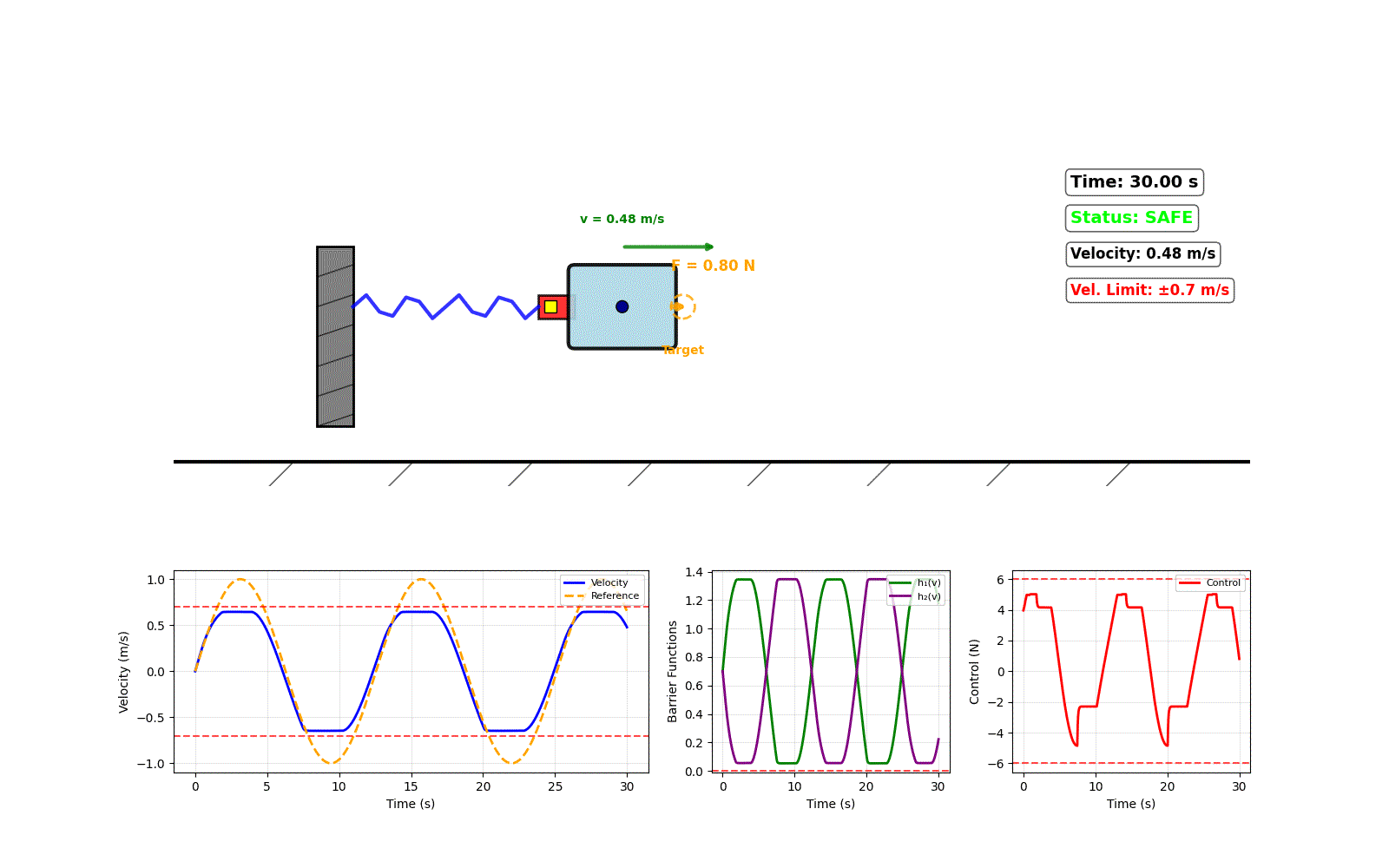
- Stable Tracking: A Control Lyapunov Function (CLF) ensures the system reliably follows a desired trajectory.
- Guaranteed Safety: A Control Barrier Function (CBF) enforces safety constraints, such as velocity or torque limits, which are never violated.
- Robustness: A specially designed switching law actively compensates for the combined effects of all model uncertainties, keeping the system stable and safe.
This unified approach prioritizes safety while robustly achieving high-performance tracking, even when the underlying model is inaccurate.
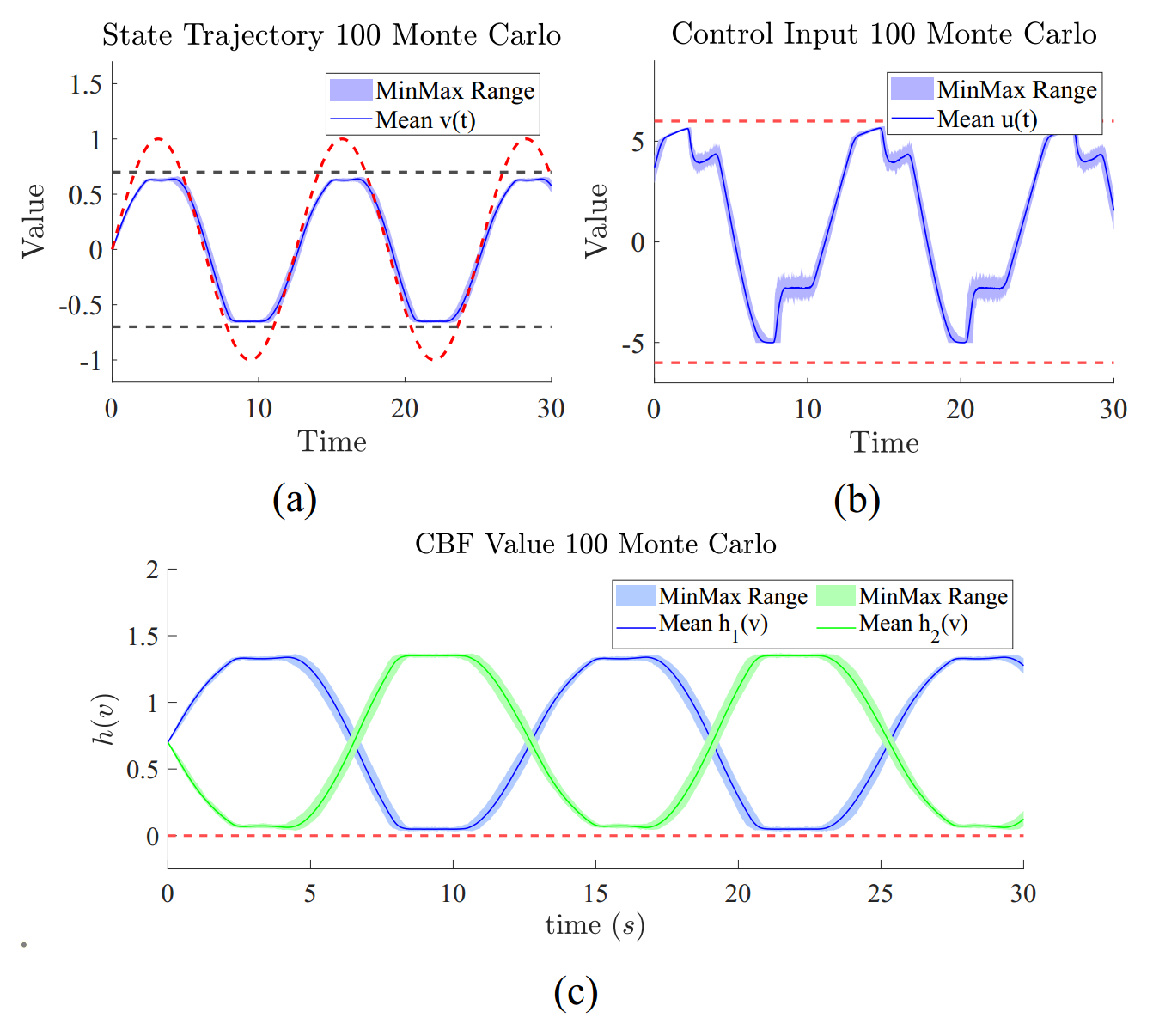
Stress-Testing for Robustness
To prove the robustness of our framework, we conducted a Monte Carlo simulation. We ran our controller 100 times on the same tracking task. In each trial, we randomly altered the true physical parameters of the simulated system by up to ±15% of their nominal values, while keeping the controller's model fixed.
The results below show the range of outcomes. Despite significant, random modeling errors, our controller consistently kept the system stable and, most importantly, never violated the safety constraints. The narrow performance band demonstrates the controller's high level of robustness to uncertainty.
BibTeX
@INPROCEEDINGS{11151463,
author={Sinaei, Kasra and Ebeigbe, Donald},
booktitle={2025 IEEE Conference on Control Technology and Applications (CCTA)},
title={Safe Robust Control of Nonlinear Systems with Uncertain Regressor and Parameter Vector},
year={2025},
volume={},
number={},
pages={982-987},
keywords={Robust control;Uncertainty;Monte Carlo methods;Perturbation methods;Numerical simulation;Vectors;Robustness;Numerical models;Safety;Trajectory},
doi={10.1109/CCTA53793.2025.11151463}
}